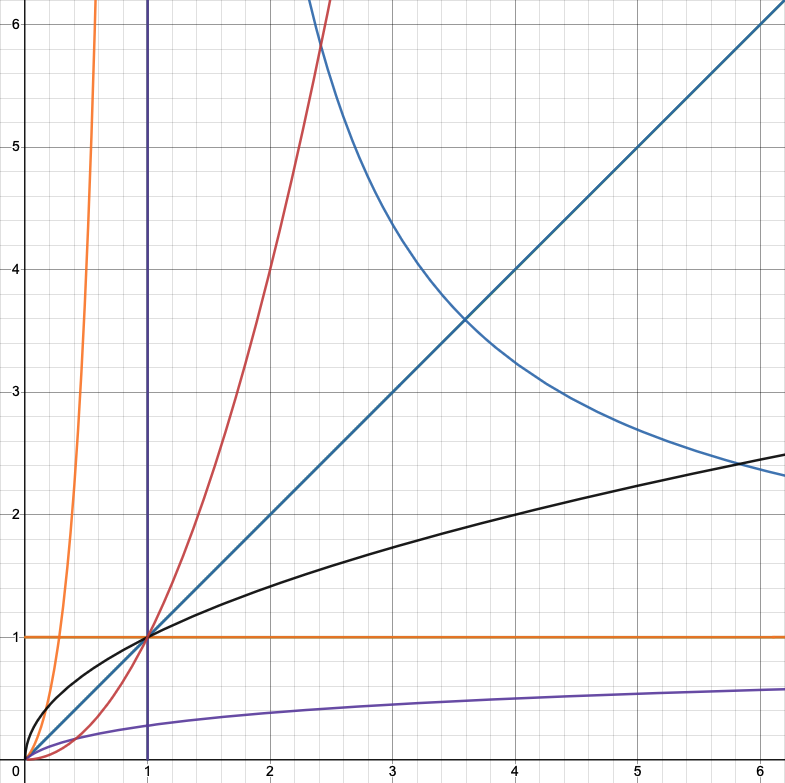
All curves are normalized so f(1)=1—which is exactly why they must meet at (1,1), the B=1 fixed point.
y = x → direct proportion (identity mirrors itself).
y = 1/x → inverse relation (complements meet at unity).
y = x² → curvature/intensification (gravity/localization).
y = √x → relaxation/diffusion (space equalizing).
y = e^{x-1} → becoming/growth from unity (Spirit-mode).
y = ln(x)+1 → recognition into unity (Father-mode).
y = 1 and x = 1 → presence/identity axes.
Why (1,1) is inevitable: for any admissible relational law y=f(x) that’s coherent at unity, the normalization constraint f(1)=1 makes (1,1) a fixed point. In Perfect Logic that’s just the statement B = 1 ⇔ 1 = 1 — ground and expression coincide, so every lawful relation touches the same point of complete proportion.